Rebecca S. Lindsay's Tutoring Service

Dear Lois:I would get along just fine in geometry if it weren't for triangles--like you know, like when you have to find like the area which is like A = 1/2 bh because I always forget to multiply by like 1/2. So why do we always have to multiply by 1/2?Puzzled

Dear Puzzled:How about if I show you a little magic trick--like how to turn a triangle into a rectangle? Presto-chango! The hand is quicker than the eye!

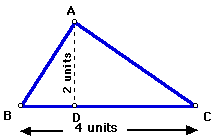
First, I take a triangle--just an ordinary triangle--base 4 units, height 2 units. Take a good look at it to make sure that it is not a trick triangle. Okay? Now watch closely!

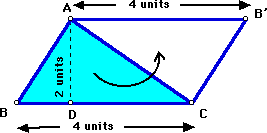
Next, I turn the triangle into two triangles and rotate the second triangle into place to create a parallelogram. Zap! Zap! Zam! Alacazam! Wasn't that neat?

Notice what happened to the base and height of our parallelogram. That's right--nothing! The base of the parallelogram is 4 units and the height is 2 units, just like our triangle. But the two triangles cover up twice as much area, or space, as one triangle.

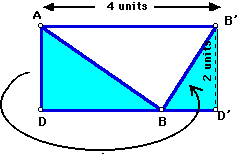
Now I'll chop off the ABD part of the parallelogram and move it into place to make a rectangle. Abracadabra!

Are the base and height of the rectangle still the same as the base and height of the triangle? (Say, yes.)

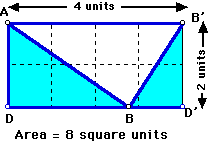
What is the area of the rectangle? That's easy to calculate. Just multiply base times height, or length times width.

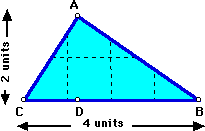
Area of rectangle = length X widthArea of rectangle = 4 units X 2 unitsArea of rectangle = 8 square units

And the area of the triangle? Remember: to make the parallelogram and the rectangle, we doubled the triangle. So now we have to multiply the area of the rectangle by 1/2 to get back to the area of the triangle.

Area of triangle = 1/2 base X heightArea of triangle = 1/2 X 8 square unitsArea of triangle = 4 square units

Can you use your imagination and see where the 4 square units are?

Return to Home page.