Hi:Can you tell me how to work out the area of a five or more sided polygon?Nasrin

Dear Nasrin:Yours must be the FAQ of the year. Hardly a month goes by that I don't receive a request for the area of a polygon, sometimes with quite a few special circumstances involved. For you and all those other curious math students out there, I will explain some of the basic concepts involved in calculating the area of both an irregular polygon and a regular polygon.

Any convex polygon, no matter how many sides, can be divided into triangles just by choosing a vertex and drawing diagonals from that vertex to every other vertex. As you can see by studying the illustration, the number of triangles that can be drawn is always two less than the number of sides.

The area of each triangle can then be calculated and the individual areas added to obtain a total. Watch how it works with this irregular pentagon.

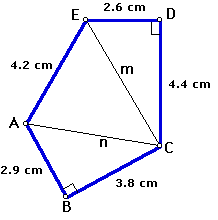
The pentagon is divided into three triangles.

Then the area is computed (See below) for each individual triangle using the formula:

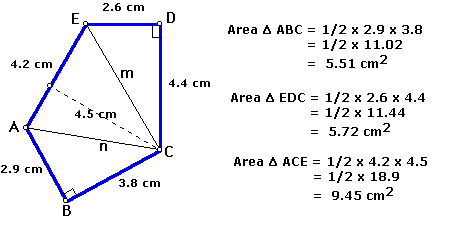
Now the areas of the three triangles are added to obtain the total area of the pentagon.

If you have gotten this far and still want to learn about finding the area of a regular polygon, study the explanation below. Finding the area of a regular polygon is more difficult because of the math involved, but also easier because the whole operation can be done with a single formula. Before you can use the formula, however, you must understand the special parts of a regular polygon--the center, the radius, and the apothem.

Return to Home page.

"Ask Lois Terms" © 2001 Lindsay-Livingston