Dear Lois:Could you explain why you add the exponents when you multiply powers of ten? Also why you subtract the exponents when you divide powers of ten?Cindy

Dear Cindy:I must admit that the methods for multiplying and dividing exponents are some of the strange, but true, rules of mathematics. Why would anyone add when they really meant to multiply or subtract when they wanted to divide? But we do. These rules apply to any kind of exponents, not just powers of ten, so first let's look at exponents in general.

EXPONENTS

An exponent simply tells us how many times we are going to multiply a number or variable by itself. For instance, when we see 34, the 4 stuck up there in the air like that tells us to multiply 3 by itself 4 times.




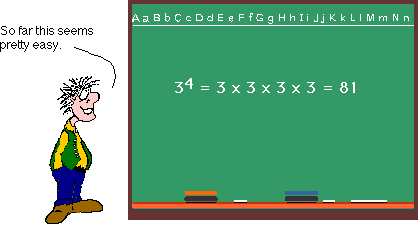
But suppose we have a variable with an exponent, such as X5.

Now, X is a mystery number. Nobody knows who X is or how much she is worth. We can speculate about X's value, but until we find out the value of X, we can only show X5. If we ever do find out what X is worth, then we can multiply X's value by itself five times.








MULTIPLYING EXPONENTS

Ready to take the next step? Let's think about multiplying X5 by X3. We are really saying that we want to multiply X by itself five times, then by itself three times more--or eight times in all.



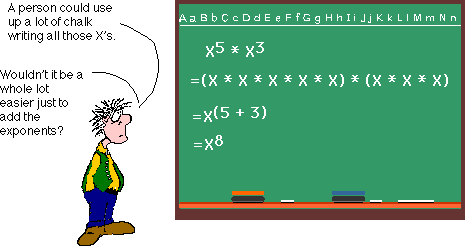
So you see, when we are multiplying with exponents, adding the exponents is just a shortcut.



MULTIPLYING POWERS OF 10

The same principle is true for multiplying powers of ten. 103 X 102 just means to multiply ten by itself 3 times, then 2 times more, or 5 times in all.



DIVIDING EXPONENTS

Subtracting exponents when we divide them is also just a short cut. Notice how the X's are stacked up in the problem below. We can arrange them so that we match X's in the numerator with X's in the denominator. Since any number (or variable) divided by itself equals 1, the matched X's can be eliminated. (Some people call this canceling.) The X's that are left over can be multiplied together (that is if we ever find out what X is worth.)



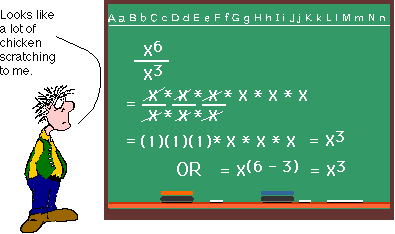
DIVIDING POWERS OF 10

Would you like to see that done with powers of ten? Works just the same way. See below.


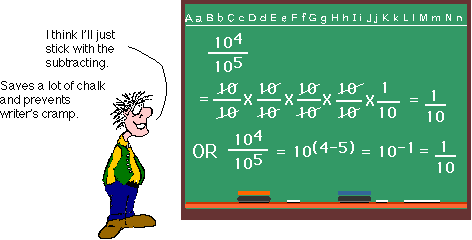
I hope, Cindy, that this explanation has been of help. Best of luck in your studies. Love, Lois



Return to Home page.

"Ask Lois Terms" © 2001 Lindsay-Livingston