Rebecca S. Lindsay's Tutoring Service

Dear Students:In Issue 25 we took up the problem of pulling a pair of matching socks from a sock drawer. And although we were able to get a pair of matching socks in fairly short order, we sent poor Sam off to school wearing khaki pants, a red shirt and a pair of yellow socks with purple stripes.

Suppose, however, Sam likes to arrive at school wearing a pair of socks that aren't having an argument with the rest of his clothes . What is the probability that Sam will be able to pull a pair of white sports socks with red stripes out of his drawer in just two pulls?

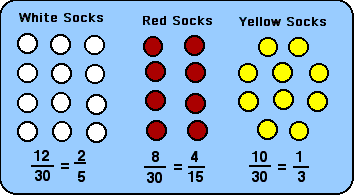
The first thing Sam needs to do in determining probability is to find the total number of socks that he has. The last time he counted there were 12 white sports socks with red stripes, 8 red socks with blue dots, and 10 yellow socks with purple stripes in his sock drawer. That would make 30 socks in all, all jumbled in the drawer since Sam never takes the time to roll matching socks together into pairs. We call the 30 socks in Sam's sock drawer the sample space.

The event that Sam wants to happen is that he pulls two white socks in a row, so pulling a white sock on the first pull and another white sock on the second pull would be called favorable outcomes. Any other outcomes, such as pulling yellow socks or red socks on either pull aren't going to help Sam, so we aren't interested in those outcomes.

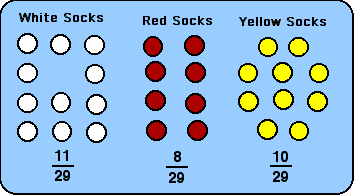
Let's reduce the socks to colored dots to make the problem manageable. As you can see, there are 12 chances out of thirty that Sam will pull out a white sock on the first pull. We make the ratio 12/30 to represent the probability that Sam will get a white sock. We can reduce 12/30 to 2/5 if we want.

Now there are only 11 white socks in Sam's drawer, but still 8 red and 10 yellow ones for a total of 29 socks in the drawer. Sam has 11 chances out of 29 of pulling out a white sock on the second time he rummages in the drawer. We call Sam's second pull a dependent event because what happened with the first pull influences what happens with the second pull. We make up a second ratio of 11/29 to show the probability of pulling a white sock on the second draw.

To calculate the probability that Sam will come up with two white socks on the first two pulls, we multiply the ratio from the first pull with the ratio of the second pull and come up with a third ratio: 132/870. This ratio tells us that if Sam pulls one sock and then a second sock from his sock drawer 870 times, on 132 of those times he is likely to come up with a pair of white socks. Or if we want, we can simplify 132/870 to 22/145 and think that if Sam pulls two socks out 145 times, he will get a white pair about 22 times. We could demonstrate with a tree diagram, but it would take up a tree-mendous amount of space!

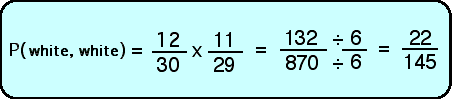
Sure makes a good case for rolling your socks into pairs in the first place and turning the light on instead pulling out socks in the dark.

Return to Home page.