In this puzzle you are dealing with trick triangles.

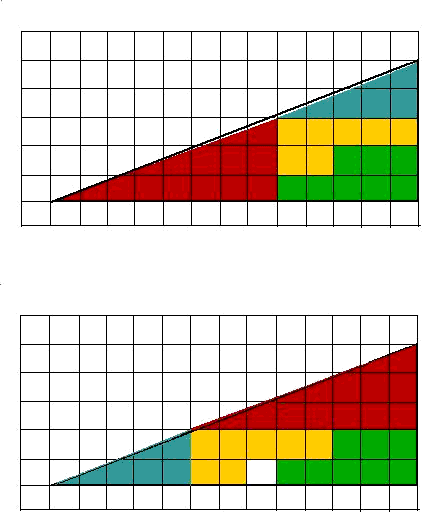
The two triangular puzzle pieces don't fit exactly over the whole-area triangle; but you can't see that, because the whole-area triangle is not drawn in on the puzzle. Notice on the diagrams below that I have carefully drawn the whole-area triangle in.

The two smaller triangles don't fit because they don't have the same slope, or slant, that the whole-area triangle has.

The slopes of the triangles can be calculated by making fractions using their heights over their bases.

As you can see, the slopes are very close together, close enough to fool the human eye into thinking that the slanted lines on the triangles are all running on top of each other.

But, actually, they aren't. The smallest triangle is steeper than the whole-area triangle, and the larger triangle is not as steep as the whole-area one.

If you look carefully at the first diagram, you will see that there is a gap between the edges of the two little triangles and the whole-area one. That gap has an area of--you guessed it--0.5 square units! Ah, ha! Half of the missing square-unit piece!

Now look at the second diagram. When the triangle pieces are switched, they cover not only the 0.5 sq. unit gap shown in the first diagram, but also extend outside the whole area triangle and cover an area of 0.5 square units there. Ah, ha! The second half of the missing square-unit piece!

Since the puzzle pieces cannot cover any more area that 32 sq. units, the "hole" appears.

So, there you have it. The hole came from the 0.5 sq. unit "gap" and the 0.5 sq. unit "overlap" covered by the triangular puzzle pieces.

Return to Home page.

"Ask Lois Terms" © 2000 Lindsay-Livingston